What is a number again?
By
Dan Christensen
(Revised: 2016-11-01)
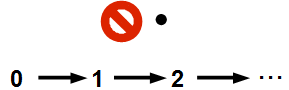
What is a number? If we could see them, what might the set of natural numbers look like? You might picture an endless line of nodes (numbers) connected by one-way arrows, starting at 0. Next, is 1, then 2 and so on.
(For reasons that will be apparent below, I call this the main sequence.)
From this diagram, we can see that:
1. 0 is a number (the first number here).
2. Every number has a unique next number.
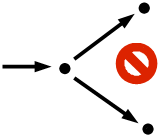
3. No two numbers have the same next number.
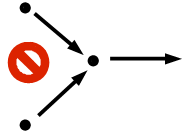
4. No number has 0 as its next number (0 is the first number).
5. No non-empty, proper subset of the natural numbers is completely disconnected from the remaining numbers.
It all seems so obvious, so self-evident, but... so what? The thing is, this short list of “obvious and self-evident” properties characterize the set of natural numbers to the extent that from these properties alone, we can (in theory) derive all of number theory, algebra and calculus. Yes, at its base, mathematics is that simple!
Let's now translate this list of properties into the language of DC Proof.
1. 0 is a number:
0 e n
2. Every number has a unique next number:
ALL(a):[a e n => next(a) e n]
3. No number has 0 as its next number:
ALL(a):[a e n => ~next(a)=0]
4. No two numbers have the same next number:
ALL(a):ALL(b):[a e n & b e n => [~a=b => ~next(a)=next(b)]]
or equivalently...
ALL(a):ALL(b):[a
e
n
&
b e
n
=>
[next(a)=next(b)
=> a=b]]
5. No number exists outside the main sequence.
ALL(a):[Set(a)
& ALL(b):[b e a => b e n] (a is a subset on n)
& 0 e a (a is the main sequence)
& ALL(b):[b e a => next(b) e a]=> ~EXIST(b):[b e n & ~b e a]] (no element of n exists outside the main sequence)
or equivalently...
ALL(a):[Set(a)
& ALL(b):[b e a => b e n]
& 0 e a
& ALL(b):[b e a => next(b) e a]=> ALL(b):[b e n => b e a]] (switched quantifier)
Again, no non-empty,
proper subset of the natural numbers is completely disconnected from the
remaining numbers.
Formal Proof (149
lines).
It can be shown that if set n', element 0' and function next' satisfy the above axioms (with the obvious substitutions in the above axioms), then n and n' would have to be an identical “copy” of one another. The structures of n and n' will be identical, only the names will have been changed, i.e. n would be order-isomorphic to n'. (This is not true of algebraic structures in general.)
Informally, we can match up the elements of n and n' quite naturally as follows:
0 ↔ 0'
next(0) ↔ next'(0')
next(next(0)) ↔ next'(next'(0'))
...and so on.
This matching up would be uniquely given by the function f mapping n to n' such that:
ALL(a):[a e
n => f(a) e
n']
&
f(0)=0'
&
ALL(a):[a e
n => f(next(a))=next'(f(a))]
Formal Proof (723 lines)
If can be further shown that f would be a bijection mapping n to n'. Formal Proof (188 lines)
Finally, it can be shown that f would preserve the successor relation on each set:
ALL(a):ALL(b):[a e n & b e n => [next(a)=b <=> next'(f(a))=f(b)]]
Formal Proof (167 lines)